ЎЎЎЎФӯҳЛ(biЁЎo)о}ЈәғЙЭҶЧФРРЬҮФЪРРсӮ•rһйКІГҙІ»•юө№����Јҝ ҝҙНкУЦқqЦӘЧRАІЈЎ
ЎЎЎЎЧФРРЬҮ¬F(xiЁӨn)ФЪКЗәЬЖХНЁөДТ»·NҪ»НЁ№ӨҫЯ��ЎЈ“ю(jЁҙ)Оч·ҪОД«IУӣЭd�����Ј¬ЛьЧоФзКЗТ»·NИзҲD1ұ»·Qһй“әГсR”ЈЁdandy horseЈ©өД»¬РР№ӨҫЯ���Ј¬З°ЯMөД„УБҰКЗИЛөДД_ФЪөШЙПРРЧЯ�����Ј¬ЯҖКЗ1817ДкТ»О»ГыҪРөВИRЛ№ЈЁBaron von DraisЈ©өДөВҮшИЛ°l(fЁЎ)ГчөД���Ј¬ИЎөГБЛҢЈАыЎЈәуҒнҪӣ(jЁ©ng)Я^ФS¶аёДЯMЈ¬ЦұөҪ19КАјoЦРИ~ІЕ°l(fЁЎ)Х№өҪ¬F(xiЁӨn)ФЪөДДЈҳУ�Ј¬І»Я^“ю(jЁҙ)Ў¶ЗеіҜТ°К·ҙуУ^Ў·УӣЭdЈә“ьSВДЗfЛщЦЖлpЭҶРЎЬҮТ»ЭvЈ¬йLИэіЯУа�Ј¬ҝЙЧшТ»ИЛЈ¬І»нҡНЖНм����Ј¬ДЬЧФРРЎЈРР•r�Ј¬ТФКЦНмЭSЕФЗъ№ХЈ¬„tҸН(fЁҙ)РРИзіх�Ј¬лSЧЎлSНмИХЧгРР°ЛК®АпЎЈ”УЙҙЛҝЙТҠ�����Ј¬ЛыЦЖФмөДЧФРРЬҮ��Ј¬З°әуёчУРТ»ӮҖЭҶЧУ��Ј¬тTЬҮИЛКЦ“uЭSЕФЗъ№Х����Ј¬ЬҮҫНДЬЗ°ЯM��Ј¬Я@КЗК·БПЧоФзУӣЭdөДЧФРРЬҮЎ�ЈҝЙТҠЗеіҜИЛьSВДЗfЈЁ1656-ЈҝЈ©әЬФзҫН°l(fЁЎ)ГчБЛоҗЛЖУЪЧФРРЬҮөДСbЦГ����Ј¬¶шЗТІ»КЗУГД_өЕ¶шКЗУЙКЦ“u„УЗъұъЗ°ЯMЎЈ
ЎЎЎЎ“әГсR”
ЎЎЎЎұИьSВДЗfҙуТ»ҡqөДЗеіхФ~ИЛј{МmРФөВЈЁ1655Јӯ1685Ј©ФЪЛыөД№PУӣРЎХfЎ¶ңOЛ®НӨлsЧRЎ·ЦРУРТ»¶ОУӣЭdЈә“ОдәоДҫЕЈБчсR��Ј¬№ЕУРСФКЗРЎЬҮХЯ�����ЎЈОчИЛУРЧФРРЬҮ�Ј¬З°ЭҶҪ^РЎЈ¬әуЭҶҪ^ҙу��Ј¬ТФёЯЕRПВЦ®„Э�����ЎЈ№КЖҪөШТФөГЧФРР�ЎЈ»тјҙДҫЕЈБчсRәх�ЎЈ¶шҝІЗъХЫЈ¬ҙуЩMИЛБҰТІ����ЎЈ”ҝЙТҠФЪЗеіх��Ј¬Оч·ҪӮчҪМКҝҫНТСҪӣ(jЁ©ng)°С®”(dЁЎng)•rОч·ҪөДЧФРРЬҮӮчөҪЦРҮшҒнБЛ�ЎЈЯ@АпХfУЙУЪЗ°ЭҶРЎәуЭҶҙу���Ј¬ДЬүт“ТФёЯЕRПВ”ЛщТФЖҪөШДЬүтЧФРРөДХf·Ё�����Ј¬ҸДБҰҢW(xuЁҰ)ЙПКЗӣ]УРөААнөД����ЎЈЯ@ФЪ®”(dЁЎng)•rБҰҢW(xuЁҰ)ҢW(xuЁҰ)ҝЖЯҖІ»іЙКм���Ј¬БҰҢW(xuЁҰ)ЦӘЧRТІІ»ЖХј°өДЗйРОПВөДТ»·NГЙГБөДІВПл���Ј¬КЗҝЙТФАнҪвөД���ЎЈЦБУЪХfөҪёЯөНІ»ЖҪөДөАВ·ЙП�����Ј¬ҙуЩMИЛБҰ�Ј¬КЗҝЙТФАнҪвөДЎЈј{МmРФөВМбөҪөДЧФРРЬҮ�Ј¬ҙујsРОИзҲD2»тҲD3Ј¬І»Я^УГжң—lӮч„УөДЧФРРЬҮ�Ј¬ҙујsТӘөҪ19КАјoД©ІЕЖХұйК№УГЎЈ
ЎЎЎЎЗ°ЭҶРЎ¶шәуЭҶҙуөДЧФРРЬҮ
ЎЎЎЎЧоФзУРжң—lӮч„УөДЧФРРЬҮ
ЎЎЎЎ¬F(xiЁӨn)Ҫс�Ј¬ҢҰУЪТ»°гИЛҒнХfЈ¬тTЧФРРЬҮКЗЭp¶шТЧЕeөДКВЗй�ЎЈФзЖЪөДСРҫҝҙу¶ајҜЦРЧўТвУЪИзәОјУЛЩөДҶ–о}ЎЈКВҢҚТСҪӣ(jЁ©ng)ЧCГч��Ј¬ЛьКЗТ»·NЧоКЎБҰЧоғһ(yЁӯu)РгөД·ЗҷC„УҪ»НЁ№ӨҫЯ���ЎЈІ»Я^ТӘЦvЗеіюРРЯMЦРөДЧФРРЬҮһйКІГҙІ»ө№өДҶ–о}����Ј¬јҙЧФРРЬҮөДҝШЦЖөДҶ–о}���Ј¬ҝЙІ»ДЗГҙәҶҶО��ЎЈЯ@ҫНКЗЛщЦ^өД“ЧФРРЬҮ·Җ(wЁ§n)¶ЁРФ”өДҶ–о}����Ј¬јҙУРғЙӮҖЭҶЧУЦ§ЖрҒнөДЧФРРЬҮЈ¬ФЪРРЯM•rһйКІГҙҫУИ»·ЗіЈ·Җ(wЁ§n)®”(dЁЎng)І»•юғAёІ��ЈҝТ»°Щ¶аДкҒнЯ@н—СРҫҝОьТэБЛФS¶аЦшГыөДБҰҢW(xuЁҰ)јТ����ЎўОпАнҢW(xuЁҰ)јТДЛЦБ”ө(shЁҙ)ҢW(xuЁҰ)јТ…ўјУЈ¬АЫУӢ°l(fЁЎ)ұнөДУРГыөДХ“ОД�����Ј¬°ьАЁТФУў���ЎўөВЎў·Ё���Ўў¶нЎўТвҙуАыөИёч·NХZСФөДХ“ОД��Ј¬ФЪ°ЩЖӘТФЙП�����Ј¬ЖдЦРЯҖУРІ©Кҝ��ЎўҙTКҝәНҢW(xuЁҰ)КҝөД®…ҳI(yЁЁ)Х“ОДЈ¬МШ„eКЗ1897Дк·ЁҮшҝЖҢW(xuЁҰ)Фә�����Ј¬ЯҖһйЦ®ФO(shЁЁ)БўЯ^Т»ҙО‘ТЩpЈЁPrix Fourneyron competitionЈ©ЎЈБоИЛу@®җөДКЗ��Ј¬ЖщҪсЯ@ӮҖҶ–о}әЬлyХfТСҪӣ(jЁ©ng)ЧоәуҪвӣQБЛЈ¬ИЛӮғЯҖФЪА^Аm(xЁҙ)СРҫҝ�����ЎЈ
ЎЎЎЎҸД1869ДкУўҮшҪЬіцөДБҰҢW(xuЁҰ)јТЎў№ӨіМҺҹәНҹбБҰҢW(xuЁҰ)јТМmҪрЈЁWilliam John Macquorn Rankine�Ј¬1820-1872)°l(fЁЎ)ұнБЛТ»ЖӘо}һйЎ¶ЧФРРЬҮЯ\„УөД„УБҰҢW(xuЁҰ)ФӯАнЎ·ЈЁOn thedynamical principles ofthe motion of velocipedesЈ©����ЎЈКЗУ‘Х“ЧФРРЬҮЖҪәвәНс{сӮөДЧоФзөДОДХВ����ЎЈДЗЖӘОДХВЦ»КЗ°л¶ЁРФөДУ‘Х“���Ј¬ҢҰәуИЛөДУ°н‘І»ҙу�����ЎЈЖдәу���Ј¬ИгЛ№ЈЁG. G. R. RouthЈ©(1899Дк)�Ўў»ЭЖХ¶ъЈЁFrancis WhippleЈ©ЈЁ1899ДкЈ©¶јПаА^°l(fЁЎ)ұнХ“ОД�����ЎЈҝЁ·ЁБ_ЈЁE.CarvalloЈ©ЈЁ1899-1901ДкМбҪ»БЛ300н“өДХ“ОД���Ј¬һйҙЛ«@өГ·ЁҮшҝЖҢW(xuЁҰ)ФәөД‘ТЩp�����ЎЈЖдәуЈ¬өВҮшЦшГыөДОпАнҢW(xuЁҰ)јТЛчД«·ЖЈЁArnold SommerfeldЈ©ЈЁ1910ДкЈ©���ЎўөВҮшЦшГы”ө(shЁҙ)ҢW(xuЁҰ)јТҝЛИRТтЈЁFelix KleinЈ©(1910Дк)��ЎўЦшГыБҰҢW(xuЁҰ)јТиFДҫРБҝЖәН—оЈЁTimoshenkoand YoungЈ©��ЎўБҰҢW(xuЁҰ)јТаҮ№юНРЈЁJ. P. Den HartogЈ©ЈЁ1948ДкЈ©¶јФЪЛыӮғөДЦшЧч»тХ“ОДЦРХ“ј°ЧФРРЬҮөД·Җ(wЁ§n)¶ЁРФҶ–о}ЎЈФЪЛыӮғЦ®әуУРёь¶аөДИЛУ‘Х“�����Ј¬ЖдЦРУРИфёЙЖӘҢW(xuЁҰ)О»Х“ОДЎЈ
ЎЎЎЎФЪ1969ДкөҪ1970ДкЯ@Т»°ЩДкйg°l(fЁЎ)ұнөДЯ@ФS¶аХ“ОД�Ј¬ҢҰЧФРРЬҮРРсӮөД·Җ(wЁ§n)¶ЁРФ���Ј¬МбіцБЛёч·NДЈРНЈ¬ТІБРіцБЛІ»Н¬оҗРНөДОў·Ц·ҪіМҪM�ЎЈІ»Я^ЖдЦРУ°н‘ұИЭ^ҙуөДТ»·NХf·Ё�����Ј¬ҫНКЗЧФРРЬҮЗ°ЭҶөДНУВЭР§‘Ә(yЁ©ng)�Ј¬ТФЦБУЪФЪФS¶аНЁЛЧЧxОпЦР¶јТФЯ@·NУ^ьcҒнҪвбҢЧФРРЬҮөД·Җ(wЁ§n)¶ЁРФЎЈ
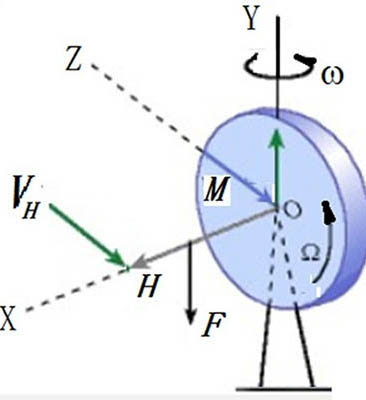
ЎЎЎЎҢҰУЪНУВЭР§‘Ә(yЁ©ng)ЧФРРЬҮ·Җ(wЁ§n)¶ЁРФөДҪвбҢ�����ЎЈОТӮғәҶТӘөШҒнЧцХfГч���ЎЈДгДГТ»Г¶УІҺЕ��Ј¬ЧҢЛьФЪЖҪГжЙПқL„УЈ¬Из№ыЖрКј•rҝМЧҢЛьВФОўғAРұЈ¬ұИ·ҪХfИзПВҲDҲDКҫғAПтЧуӮИ(cЁЁ)��Ј¬ДгҫН•ю°l(fЁЎ)¬F(xiЁӨn)�Ј¬Ль•юПтғAРұөДЯ@·Ҫ№ХҸқЈ¬®”(dЁЎng)ғAРұҪЗЧғөГУъҙу•r���Ј¬№ХҸқөДЗъВКТІУъҙуЈ¬ЧоәуөҪғAө№һйЦ№�ЎЈ

ЎЎЎЎқL„УөДУІҺЕ
ЎЎЎЎ¬F(xiЁӨn)ФЪОТӮғ°СЯ@ӮҖ¬F(xiЁӨn)ПуҸДБҰҢW(xuЁҰ)ЙПјУТФ·ЦОц��Ј¬ғAРұөДУІҺЕКЬТ»ӮҖУЙЧчУГФЪЦРРДөДЦШБҰәНөШГжЦ§“ОБҰЛщРОіЙБҰЕјөДЧчУГ�Ј¬ҫНКЗФЪЯ@ӮҖБҰЕјЧчУГПВУІҺЕқL„УІЕ°l(fЁЎ)Йъ№ХҸқЎЈ¬F(xiЁӨn)ФЪОТӮғ°СТФЙПқLУІҺЕөДЗйӣr»ҜҡwһйҲD5����Ј¬БоҲDЦРөДҲAұPһйУІҺЕЈ¬ЛьТФҲAұPөД·ЁҫҖһйOH���Ј¬ҲAұPЛщКЬөДБҰҫШТФБҰFЕcЦ§“ОМҺЕcЦ®·ҪПтПа·ҙөДБҰЈ¬ЖдБҰҫШөДҙуРЎТФMұнКҫЎ����Ј¬F(xiЁӨn)ФЪУГОХЖрҒнөДУТКЦЛДЦёөД·ҪПтұнКҫБҰҫШЧчУГөДРэЮD(zhuЁЈn)·ҪПтЈ¬ДЗГҙЙмЦұөДДҙЦёөД·ҪПтұгКЗҲAұP·ЁҫҖHРэЮD(zhuЁЈn)өД·ҪПт�����Ј¬ТІҫНКЗХfҲAұPА@YЭSТФҪЗЛЩ¶ИωҒнРэЮD(zhuЁЈn)����Ј¬Я@ҫНКЗҲAұP№ХҸқЛщТӘЗуөДҪЗЛЩ¶ИЎЈҫНКЗХf��Ј¬РэЮD(zhuЁЈn)ҲAұP�����Ј¬Из№ыІ»КЬНвБҰҫШ���Ј¬Ль•ю°ҙХХ‘TРФ����Ј¬·ҪПтІ»ЧғөШЮD(zhuЁЈn)„УПВИҘ���Ј¬Из№ыКЬТ»ӮҖНвБҰҫШөДЧчУГЈ¬ЛьөДЮD(zhuЁЈn)„У·ҪПт•юЮD(zhuЁЈn)„У�����Ј¬ЖдЮD(zhuЁЈn)„УөД·ҪПтөД°ҙХХЙПКцУТКЦ·Ё„t�Ј¬¶шЗТЮD(zhuЁЈn)„УөДҪЗЛЩ¶ИωөДҙуРЎКЗЕcБҰҫШMөДҙуРЎіЙұИАэөДЈ¬Я@ҫНКЗЛщХfөДНУВЭР§‘Ә(yЁ©ng)ЎЈ
ЎЎЎЎКмПӨБЛТФЙПөДҪY(jiЁҰ)№ы����Ј¬ОТӮғҒнУ‘Х“НУВЭР§‘Ә(yЁ©ng)ИзәОДЬүтК№ЧФРРЬҮРРсӮ·Җ(wЁ§n)¶ЁЎЈФO(shЁЁ)ФЪРРЯM•rЧФРРЬҮУыПтЧуӮИ(cЁЁ)ғAө№Ј¬јҙЗ°ЭҶПтЧуғAРұ��Ј¬Я@•rтTЬҮИЛІЩҝv°СКЦК№З°ЭҶПтЧуЮD(zhuЁЈn)Ј¬Я@Па®”(dЁЎng)УЪҪoЗ°ЭҶТ»ӮҖПтЧуРэЮD(zhuЁЈn)өДБҰҫШ����Ј¬ФЪЯ@ӮҖБҰҫШЧчУГПВ����Ј¬ёщ“ю(jЁҙ)УТКЦ¶Ё„tЈ¬З°ЭҶ•юУЙғAРұПтЦұБў·ҪПтЯ\„У��ЎЈН¬ҳУИзЧФРРЬҮУыПтУТғAө№���Ј¬јҙЗ°ЭҶПтУТғAРұ�Ј¬Я@•rтTЬҮИЛНЁЯ^°СКЦК№З°ЭҶПтУТЮD(zhuЁЈn)����Ј¬Я@Па®”(dЁЎng)УЪҪoЗ°ЭҶТ»ӮҖПтУТРэЮD(zhuЁЈn)өДБҰҫШЈ¬ФЪЯ@ӮҖБҰҫШЧчУГПВЈ¬ёщ“ю(jЁҙ)УТКЦ¶Ё„t�����Ј¬З°ЭҶ•юУЙғAРұПтЦұБў·ҪПтЯ\„У�����ЎЈУЙҙЛ�����Ј¬ЧФРРЬҮЧФИ»•ю·Җ(wЁ§n)¶ЁөШПтЗ°РРсӮ����ЎЈ

ЎЎЎЎУТКЦ¶Ё„t
ЎЎЎЎҲAұPКЬБҰҫШөДЯ\„УКҫТвҲD
ЎЎЎЎҹoХ“ҸДБҰҢW(xuЁҰ)ФӯАнЙПҒнХf��Ј¬ЯҖКЗҸДтTЬҮИЛөДҢҚлHҪӣ(jЁ©ng)тһҒнҝҙ��Ј¬ТФЙПЧФРРЬҮНУВЭР§‘Ә(yЁ©ng)өДҪвбҢ¶јКЗРРөГНЁөД��ЎЈЛщТФҪь°ЩДкЦР��Ј¬Я@·NУ^ьcБчРРұИЭ^ЖХұй����Ј¬ТФЦБУЪФЪФS¶аҝЖЖХ•шј®ЦРЈ¬ҙу°лТІКЗҪйҪBЯ@·NУ^ьcөД�ЎЈІ»Я^ҢҰУЪЯ@·Nҝҙ·Ё����Ј¬ТІУРИЛМбіц®җЧh����Ј¬ЦшГыОпАнҢW(xuЁҰ)јТЛчД«·ЖХfЈә“УЙЬҮЭҶөДҳӢ(gЁ°u)Фмҝҙіц����Ј¬НУВЭР§‘Ә(yЁ©ng)КЗәЬРЎөД��ЎЈИз№ыТӘјУҸҠНУВЭР§‘Ә(yЁ©ng)�Ј¬ҫН‘Ә(yЁ©ng)®”(dЁЎng)ұMҝЙДЬУГЦШөДЬҮЭҶөДЯ…ҫүәНЭҶМҘИЎҙъЭpөД����ЎЈјҙұгИзҙЛЈ¬Я@ҳУИхөДНУВЭР§‘Ә(yЁ©ng)ҢҰУЪПөҪy(tЁҜng)өД·Җ(wЁ§n)¶ЁРФІЕ•юУРЙЩФSөДШ•«I��ЎЈ”
ЎЎЎЎіэБЛНУВЭР§‘Ә(yЁ©ng)өДҪвбҢНв�Ј¬1948ДкиFДҫРБҝЖәН—оФЪЛыӮғЛщЦшөДЎ¶ёЯөИ„УБҰҢW(xuЁҰ)Ў·Т»•шЦРЈ¬ЯҖМбіцБЛБнНвТ»·NҪвбҢ��ЎЈЯ@ҫНКЗ��Ј¬®”(dЁЎng)ЧФРРЬҮНщТ»ӮИ(cЁЁ)ғAРұ•r�Ј¬тTЬҮИЛҫНУГ°СКЦҢўЗ°ЭҶЮD(zhuЁЈn)ПтН¬Т»ӮИ(cЁЁ)Ј¬УЙУЪЗ°ЭҶЮD(zhuЁЈn)БЛТ»ӮҖҪЗ¶И��Ј¬ЧФРРЬҮөДРРЯMҫНСШЦшА@ғAРұӮИ(cЁЁ)өДҲAЦЬ��Ј¬Я@•rлxРДБҰПтҲAЦЬНв��Ј¬ҫН•ю°СЧФРРЬҮ·цХэ���ЎЈУЙЯ@ӮҖҪвбҢ����Ј¬ҝЙТФөГіцҪY(jiЁҰ)Х“�Ј¬ЧФРРЬҮөДЛЩ¶ИУъҝм�����Ј¬Лщ®a(chЁЈn)ЙъөДлxРДБҰұгУъҙуЎЈЛщТФЧФРРЬҮРРЯMөДЛЩ¶ИУъҝмЧФРРЬҮұгУъИЭТЧҝШЦЖ���ЎЈІ»Я^�����Ј¬Я@·NҪвбҢЕcИЛӮғөДҪӣ(jЁ©ng)тһУРьcІо„e��ЎЈ®”(dЁЎng)ИЛӮғФЪЖҪөШЙП°СТ»ЭvЧФРРЬҮНЖРРөҪТ»¶ЁЛЩ¶ИІўЗТИцКЦ��Ј¬ЧФРРЬҮ•юҹoҝШЦЖөШ·Җ(wЁ§n)¶ЁөШЗ°РРТ»¶О�Ј¬Я@•r���Ј¬јҙК№ФЪЦРНҫ”_„УЛьТ»ПВ����Ј¬ЛьТІДЬүт»ШҸН(fЁҙ)·Җ(wЁ§n)¶Ё��ЎЈЯ@ХfГч���Ј¬ЧФРРЬҮұҫЙнФЪӣ]УРс{сӮөД—lјюПВұгУРДЬүт·Җ(wЁ§n)¶ЁЗ°РРөДҷCЦЖ��ЎЈ
ЎЎЎЎ1970Дк�Ј¬ФЪЎ¶ҪсИХОпАнЎ·лsЦҫЙПЈ¬УўҮшИЛҙуРl(wЁЁi)·тEЛ№ЈЁ David E.H. JonesЈ©°l(fЁЎ)ұнБЛТ»ЖӘОДХВ�����Ј¬Я@ЖӘОДХВҢҰәуҒнөДСРҫҝУ°н‘әЬҙу�ЎЈОДХВҲуөАБЛЧчХЯЧФЦЖБЛТ»Эvӣ]УРЗ°ЭҶНУВЭР§‘Ә(yЁ©ng)өДЧФРРЬҮЈЁИзПВҲDЈ©Ј¬ХХҳУДЬүт·Җ(wЁ§n)¶ЁөШРРсӮ����Ј¬ОДХВУГКВҢҚЧCҢҚБЛНУВЭР§‘Ә(yЁ©ng)ҢҰУЪЧФРРЬҮРРсӮөД·Җ(wЁ§n)¶ЁРФІ»КЗЦчТӘөДЎЈ

ЎЎЎЎтEЛ№өДҹoНУВЭР§‘Ә(yЁ©ng)өДЧФРРЬҮ
ЎЎЎЎтEЛ№өДЮk·ЁКЗ����Ј¬ФЪЖХНЁЧФРРЬҮЗ°ЭҶЯ…ЙПЈ¬ФЩФцјУТ»ӮҖЖҪРРөДЭҶЧУ��Ј¬Я@ӮҖЭҶЧУНЁЯ^Ӯч„УЕcЗ°ЭҶРэЮD(zhuЁЈn)·ҪПтПа·ҙ�Ј¬РэЮD(zhuЁЈn)ЛЩ¶ИПаН¬Ј¬Я@ҳУҸДХыуwЙПХfҫНөЦПыБЛЗ°ЭҶөДНУВЭР§‘Ә(yЁ©ng)����ЎЈұM№ЬЯ@ҳУ����Ј¬Я@ЭvЧФРРЬҮ��Ј¬ИФИ»ДЬүтРРсӮЧФИзӣ]УРИОәОА§лy�ЎЈ
ЎЎЎЎјИИ»НУВЭР§‘Ә(yЁ©ng)І»КЗЧФРРЬҮ·Җ(wЁ§n)¶ЁЗ°РРөДЦчТӘТтЛШЎЈ¶шЗТјҙК№ӣ]УРс{сӮ�����Ј¬ФЪТ»¶ЁЛЩ¶ИЦ®ПВЧФРРЬҮЗ°РРТІКЗ·Җ(wЁ§n)¶ЁөД����Ј¬УЪКЗҫНРиТӘҢӨЗуРВөДК№ЧФРРЬҮ·Җ(wЁ§n)¶ЁөДТтЛШ��ЎЈ
ЎЎЎЎЖХНЁЧФРРЬҮөДҳӢ(gЁ°u)Фм
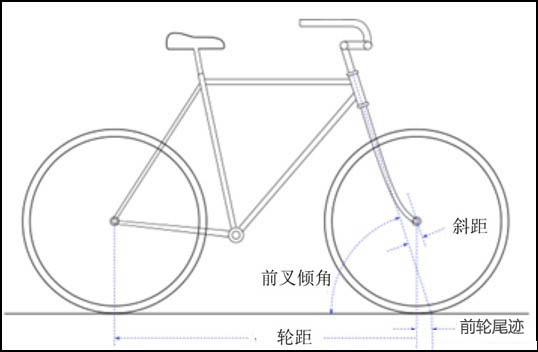
ЎЎЎЎтEЛ№ЧоәуөДҪY(jiЁҰ)Х“�Ј¬КЗ»щУЪОТӮғЖҪіЈөДҪӣ(jЁ©ng)тһЎЈ®”(dЁЎng)ОТӮғҢўЧФРРЬҮЦұБў•r���Ј¬ЧФРРЬҮЗ°ЭҶКЗПтЗ°¶шӣ]УРЖ«ЮD(zhuЁЈn)ҪЗөД����ЎЈИз№ыОТӮғЧҢЧФРРЬҮғAРұТ»ӮҖҪЗ¶И���Ј¬Па‘Ә(yЁ©ng)өШ��Ј¬ЧФРРЬҮөДЗ°ЭҶТІҫН•юлSЦ®Ж«ЮD(zhuЁЈn)Т»ӮҖҪЗ¶И�����ЎЈЯ@ХfГч��Ј¬З°ЭҶөДЦРРДёЯ¶ИКЗУЙЧФРРЬҮөДғAРұҪЗЕcЗ°ЭҶөДЖ«ЮD(zhuЁЈn)ҪЗөДәҜ”ө(shЁҙ)����ЎЈФЪЧФРРЬҮғAРұ•rЈ¬З°ЭҶ•юЖ«ЮD(zhuЁЈn)�Ј¬ТФК№З°ЭҶөДЦШРДЈЁјҙЗ°ЭҶөДЭҶРДЈ©ИЎЧоөНөДО»ЦГЎЈЦ®ЛщТФДЬүтЯ@ҳУ��Ј¬КЗәНЧФРРЬҮҳӢ(gЁ°u)ФмЦРФO(shЁЁ)УӢУРТ»ӮҖ“З°ЭҶОІЫE”өДйL¶ИУРкP(guЁЎn)���ЎЈтEЛ№УГУӢЛгҷCУӢЛгБЛЗ°ІжьcЈЁјҙЯ^З°ЭҶЦРРДЛ®ЖҪҫҖЕcЗ°ІжЦұҫҖІҝ·ЦөДСУйLҫҖөДҪ»ьcЈ©ЕcЧФРРЬҮөДғAРұҪЗәНЗ°ЭҶЖ«ЮD(zhuЁЈn)ҪЗөДкP(guЁЎn)Пө���Ј¬Лы·QЦ®һй“с{сӮҺЧәО”ЈЁsteering geometryЈ©Ј¬УРБЛЯ@ӮҖҪY(jiЁҰ)№ы�����Ј¬ҫНДЬүтҪвбҢЧФРРЬҮРРсӮөД·Җ(wЁ§n)¶ЁРФҶ–о}БЛЎЈ
ЎЎЎЎФӯҒн®”(dЁЎng)РРсӮөДЧФРРЬҮУРТ»ӮҖғAРұҪЗ•r����Ј¬ЧФРРЬҮөДЗ°ЭҶУЙУЪУР“З°ЭҶОІЫE”өДҫү№КЈ¬•юЧФ„УПтғAРұөДТ»ӮИ(cЁЁ)®a(chЁЈn)ЙъТ»ӮҖЖ«ЮD(zhuЁЈn)ҪЗ��Ј¬УЙУЪУРЯ@ӮҖЖ«ЮD(zhuЁЈn)ҪЗ����Ј¬ЧФРРЬҮҝҝЮD(zhuЁЈn)ҸқөДлxРДБҰұг•ю·цХэЎЈТтЦ®јҙК№ӣ]УРИЛс{сӮ��Ј¬ФЪТ»¶ЁөДЛЩ¶ИЦ®ПВ�Ј¬ЦұРРөДЧФРРЬҮ����Ј¬Я\„УТІКЗ·Җ(wЁ§n)¶ЁөДЎЈ
ЎЎЎЎтEЛ№ЯҖСРҫҝБЛЗ°ЭҶОІЫEһйШ“өДЗйРО�����ЎЈЯ@·NЗйРОПВ���Ј¬ЧФРРЬҮКЗәЬлyУЪс{сӮөД���ЎЈТтһй®”(dЁЎng)ЧФРРЬҮғAРұ•r�����Ј¬ЛьөДЧФИ» о‘B(tЁӨi)�����Ј¬КЗЗ°ЭҶПт·Җ(wЁ§n)¶ЁРРЯMЛщРиТӘөД·ҙ·ҪПтЖ«ЮD(zhuЁЈn)����ЎЈУЙҙЛЛыөДҪY(jiЁҰ)Х“КЗЧФРРЬҮөД·Җ(wЁ§n)¶ЁРФЦчТӘИЎӣQУЪ“З°ЭҶОІЫE”өДйL¶И����Ј¬¶шНУВЭР§‘Ә(yЁ©ng)Ц»ЖрәЬҙОТӘөДЧчУГЎЈЛщТФФЪФO(shЁЁ)УӢЧФРРЬҮ•r�����Ј¬“З°ЭҶОІЫE”өДіЯҙз���Ј¬КЗәвБҝЧФРРЬҮҝШЦЖРФДЬөДТ»ӮҖәЬЦШТӘөД”ө(shЁҙ)“ю(jЁҙ)���ЎЈ

ЎЎЎЎЗ°ЭҶОІЫEһйШ“өДЗйРО
ЎЎЎЎЦБҙЛ�Ј¬ДгТІФSХJһйкP(guЁЎn)УЪЧФРРЬҮРРсӮөД·Җ(wЁ§n)¶ЁРФҶ–о}�Ј¬‘Ә(yЁ©ng)®”(dЁЎng)ҝЙТФүm°ЈВд¶ЁБЛЎЈЖдҢҚ�Ј¬КВЗйЯҖФЪ°l(fЁЎ)Х№Ј¬өҪ2011Дк����Ј¬ОеО»ҢW(xuЁҰ)ХЯФЪЎ¶ҝЖҢW(xuЁҰ)Ў·лsЦҫЙП°l(fЁЎ)ұнБЛТ»ЖӘОДХВЎЈЛыӮғХ“ЧCФЪјИӣ]УРНУВЭР§‘Ә(yЁ©ng)ТІӣ]УРЗ°ЭҶОІЫEөД—lјюПВ��Ј¬ЧФРРЬҮХХҳУҝЙТФРРсӮөГәЬ·Җ(wЁ§n)¶Ё���ЎЈЛыӮғНЁЯ^Т»ӮҖЧФРРЬҮөДДЈ”MЖ·ЯMРРҢҚтһЈЁИзПВҲDAЈ©��ЎЈЯҖКЗФцјУТ»ӮҖЕcЗ°ЭҶ·ҙЮD(zhuЁЈn)өДЭoЦъЭҶЧУ�Ј¬ТФПыіэЗ°ЭҶөДНУВЭР§‘Ә(yЁ©ng)ЈЁИзПВҲDBЈ©�ЎЈЗ°ЭҶОІЫEКЗТ»ӮҖәЬРЎөДШ“Цө��ЎЈЯ@ҳУөД“ЧФРРЬҮ”ФЪҹoИЛІЩҝvөД—lјюПВ��Ј¬ХХҳУРРсӮөГәЬ·Җ(wЁ§n)¶ЁЈЁИзПВҲDCЈ©��ЎЈЛыӮғІўЗТҢҰЯ@ӮҖДЈРНЯMРРБЛАнХ“МҪУ‘Ј¬БРіцБЛ·ҪіМҪM���Ј¬ІўЗТУ‘Х“БЛЛьөД·Җ(wЁ§n)¶ЁРРсӮ·¶Үъ�����ЎЈЛыӮғөДСРҫҝХfГч�Ј¬ЧФРРЬҮлmИ»ҳӢ(gЁ°u)ФмәЬәҶҶО����Ј¬ө«ФЪТ»¶ЁөДЩ|(zhЁ¬)Бҝ·ЦІјЗйРОПВЈ¬ҢҚлHЙПКЗТ»·NДЬүтЧФ„УҝШЦЖЖдРРсӮ·Җ(wЁ§n)¶ЁөДҪ»НЁ№ӨҫЯ���ЎЈЖдФӯТтјИІ»КЗНУВЭР§‘Ә(yЁ©ng)����Ј¬ТІІ»КЗЗ°ЭҶОІЫE���Ј¬ҢҚФЪКЗГоІ»ҝЙСФ����ЎЈ
ЎЎЎЎӣ]УРНУВЭР§‘Ә(yЁ©ng)әНЗ°ЭҶОІЫEөДЧФРРЬҮДЈРН
ЎЎЎЎИЛӮғМҪУ‘ЧФРРЬҮөД·Җ(wЁ§n)¶ЁРФҶ–о}����Ј¬ТСҪӣ(jЁ©ng)Ҫӣ(jЁ©ng)Я^БЛТ»ӮҖ°лКАјo���ЎЈХҰТ»ҝҙҒнЈ¬ЛЖәхЯ@ҳУөДМҪУ‘ӣ]УРКІГҙҢҚУГТвБx�����ЎЈТтһйИЛјИИ»ТСҪӣ(jЁ©ng)ДЬүтЧФУЙөШс{сӮЧФРРЬҮ��Ј¬ЧФРРЬҮЦЖФмТІӣ]УРМбіцёь¶аөДТӘЗу����ЎЈЯ@ҳУөДМҪЗуЈ¬ЛЖәхУРТ»ьc•шҙфЧУөДПУТЙ���ЎЈІ»Я^����Ј¬ҢҰУЪХжАнөДМҪЗуХЯҒнХf�����Ј¬ИзДПіҜМХәлҫ°ЛщСФЈә“Т»КВІ»ЦӘ�Ј¬ТФһйЙоҗu”ЎЈҢҰУЪОҙЦӘөДКВЗйөДҢӨёщҶ–өЧөДҫ«Йс����Ј¬ХэКЗҝЖҢW(xuЁҰ)ҫ«ЙсЛщФЪЎЈБнТ»·ҪГж����Ј¬ЧФРРЬҮ·Җ(wЁ§n)¶ЁРФҶ–о}Ј¬Т»й_КјҫНКЗТ»ӮҖИЛҷCПөҪy(tЁҜng)өДҝШЦЖ·Җ(wЁ§n)¶ЁРФөДлyо}�ЎЈФЪИЛоҗҢҚ¬F(xiЁӨn)ҷCРө»ҜөДЯ^іМЦРЈ¬ИЛЕcҷCЖч���ЎўИЛЕcЖыЬҮ���ЎўИЛЕc»рЬҮЎўИЛЕcпwҷCөИөИ��Ј¬¶јУРТ»ӮҖҝШЦЖ·Җ(wЁ§n)¶ЁРФөДҶ–о}��Ј¬¶шФЪЛщУРЯ@Р©Ҷ–о}ЦР�����Ј¬ТІФSИЛЕcЧФРРЬҮөДҝШЦЖҶ–о}ёьҫЯУРМф‘р(zhЁӨn)РФ����ЎЈТтһйЛьөДҙ_ҝҙЛЖәҶҶО¶шҢҚлHЙП…sәЬҸН(fЁҙ)лs�����ЎЈТІХэТтһйИзҙЛ���Ј¬ФЪ°Щ¶аДкөДСРҫҝөДөАВ·ЙПЈ¬®җЬҠөьЖр����Ј¬РВТвҢТіцЎЈЖщҪс�Ј¬ТІәЬлyХfТСҪӣ(jЁ©ng)Я_өҪұMо^Ј¬ТІФSФЪА^Аm(xЁҙ)МҪЗуЦР����Ј¬Ль•юФЪҢҚлH‘Ә(yЁ©ng)УГЦРй_іцРВөД»Ё¶дҒнЎЈ
Н¶ёеа]ПдЈәchuanbeiol@163.com Ф”ЗйХҲФLҶ–ҙЁұұФЪҫҖЈәhttp://dstuf.com/